When considering many turns of an accelerator lattice, we observe the behaviour of a beam envelope. Hill's equation's are second order differential equations for a system with periodic focussing properties. The motion has a variable spring constant $k(s)$ which depends on the magnetic properties of the accelerator ring. If the ring has periodicity L, then so does the function $k(s)$:
\begin{equation}k(s+L) ~=~ k(s)\end{equation}
From this we can expect something similar to harmonic oscillation where the frequency and amplitude depend on the location in the accelerator ring, and show periodicity similar to that of the function $k(s)$.
The Courant-Snyder formalism assumes a solution of Hill's equation inspired by this intuition on position dependent amplitude and phase, to provide us with a set of auxiliary functions that allow us to extract the maximum information from Hill's equations. Thus we use the ansatz:
\begin{equation}x(s) ~=~ \sqrt{\epsilon \beta(s) }~ cos ( \psi (s) + \psi_0).\end{equation}
$\beta(s)$ is a position dependent amplitude, $\psi(s)$ is a position dependent phase, and $\epsilon$ is a constant known as the emittance. As Hill's equation is linear the emittance does not appear in it. $\beta(s)$ is the important variable in the Courant-Snyder formalism. Having many names such as the beta function and the beam envelope function, it has the physical meaning of amplitude, which is dependent on the position along the accelerator. It represents the focussing properties of an accelerator lattice, a small $\beta$ represents a tightly focussed lattice. We note that $\beta(s+L) = \beta(s)$.
Taking derivatives of the Courant-Snyder ansatz and substituting into the equation of motion, we get two terms; one proportional to cos and the other proportional to sin. We obtain two differential equations:
\begin{equation}\frac{1}{2} (\beta \beta'' - \frac{1}{2} \beta'^2) - \beta^2 \psi^2 + \beta^2k ~=~0,\end{equation}
\begin{equation}\beta'\psi' + \beta\psi'' ~=~ 0.\end{equation}
The latter may be integrated as:
\begin{equation} \beta'\phi' + \beta\psi'' ~=~ (\beta\psi')'. \end{equation}
We may choose the integration constant to be 1, $\beta\psi'=1$. The result for the phase function is thus:
\begin{equation}
\psi(s) ~=~ \int\limits_0^s \frac{ds}{\beta(s)},
\end{equation}
a position dependent phase, which is related to an integration of the beta function along the beam line. Knowing the beta function means that we may compute the phase function. We can eliminate the phase function from the first Courant-Snyder differential equation, to obtain a differential equation for the beta function:
\begin{equation} \frac{1}{2} \beta \beta'' - \frac {1}{4}\beta'^2 + \beta^2k ~=~1 \end{equation}
Thus we see that $\beta$ is determined by the distribution of focussing strengths along the accelerator, though we do not solve this equation in practice. We define two functions that, along with $\beta$, are called the lattice, or sometimes TWISS functions:
\begin{equation} \alpha(s) ~=~ \frac{-1}{2} \frac{d\beta(s)}{ds}, \end{equation}
and
\begin{equation} \gamma(s) ~=~ \frac{1+\alpha(s)^2}{\beta(s)}. \end{equation}
Once the lattice functions are known, the motion of a single particle through the lattice is completely defined in specifying the emittance and initial phase factor of the particle.
After some algebra we see that
\begin{equation} \epsilon ~=~ \gamma x^2 + 2 \alpha x x' + \beta x'^2. \end{equation}
Original Paper
E.D. Courant and H.S. Snyder, Ann. Phys. 3, 1 (1958)
Adapted from
[1] S. Y. Lee, Accelerator Physics, Second Edition, World Scientific, 2007
[2] H. Weidemann. Particle Accelerator Physics I: Basic Principles and Linear Beam
Dynamics. Springer, 1999
[3] R. Appleby, Beam Dynamics, Cockcroft Lectures 2011
Labels
- Accelerator Physics (5)
- Basketball (3)
- Misc. (6)
- Outreach (1)
- Panoramics (7)
- Rafique Advisor (3)
Thursday, 19 December 2013
2. Hill's Equations
Hill's equations; linearised second order differential equations for the transverse variables $x$ and $y$ in dipole and quadrupole fields within an accelerator are :
\begin{equation}x(s)'' + \left( k(s) + \frac{1}{\rho(s)^2} \right) x(s) ~=~ 0,\end{equation}
and
\begin{equation}y(s)'' - k(s) y ~=~ 0.\end{equation}
where $\rho = const$ and $k=const$ . Hills equations may be written compactly;
\begin{equation}x''+ K \cdot x ~=~ 0.\end{equation}
Where $K = k, K = (k + \frac{1}{\rho^2})$; if we write K for the constant and assume that it is constant over the accelerator, these equations appear similar to that of the a harmonic oscillator.
\begin{equation}x(s)'' + \left( k(s) + \frac{1}{\rho(s)^2} \right) x(s) ~=~ 0,\end{equation}
and
\begin{equation}y(s)'' - k(s) y ~=~ 0.\end{equation}
where $\rho = const$ and $k=const$ . Hills equations may be written compactly;
\begin{equation}x''+ K \cdot x ~=~ 0.\end{equation}
Where $K = k, K = (k + \frac{1}{\rho^2})$; if we write K for the constant and assume that it is constant over the accelerator, these equations appear similar to that of the a harmonic oscillator.
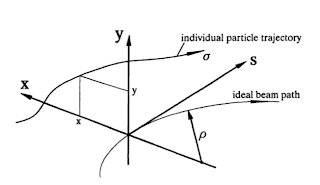
1. Coordinates
We begin by defining a curved coordinate system, the curvature $\rho$ produced by a local dipole field, and the path length along the design trajectory is $s$. The position of a particle in these coordinates is:
\begin{equation} r ~=~ \rho + x. \end{equation}
These coordinates represent deviations with respect to the ideal design orbit, we assume these deviations to be small; in reality $x$ is in the of order mm. We use the positions $x$ and $y$, and their slopes $x' = \frac{dx}{ds}$ and $y' = \frac{dy}{ds}$.
Circular coordinate system [1]
\begin{equation} \vec{R} ~=~ r \vec{x} + y \vec{z}, \end{equation}
where\begin{equation} r ~=~ \rho + x. \end{equation}
These coordinates represent deviations with respect to the ideal design orbit, we assume these deviations to be small; in reality $x$ is in the of order mm. We use the positions $x$ and $y$, and their slopes $x' = \frac{dx}{ds}$ and $y' = \frac{dy}{ds}$.
Circular coordinate system [2]
References
[1] R. Appleby. Beam Dynamics. Cockcroft Lectures 2011
[2] H. Weidemann. Particle Accelerator Physics I: Basic Principles and Linear Beam
Dynamics. Springer, 1999
Wednesday, 16 October 2013
How to Add EBooks to Android Kindle App
Having downloaded the Kindle app for Android, but was having difficulty adding ebooks to my Android's microSD card.
It is easy enough to copy ebooks in their various formats to the kindle folder on an Android external memory, however the Kindle app doesn't always recognise them.
After scouring the internet I found a simple solution;
It is easy enough to copy ebooks in their various formats to the kindle folder on an Android external memory, however the Kindle app doesn't always recognise them.
After scouring the internet I found a simple solution;
- Download the Calibre ebook manager.
- Open Calibre, and use the Add books button (top left corner) to select the required ebooks.
- Use the convert tool to convert the ebooks into .azw3 format, you can also customise the output resolution to suit your own device as well as many other options
- Copy the .azw3 files to your microSD/other storage device, placing them in the kindle/ folder.
- Open the kindle app and use the sync button (top right hand corner) to search for new ebooks. It may take a few minutes to update, depending on the size and number of books added.
Also note that Amazon Prime members can only make use of the free book 'lending' scheme if they are using a Kindle device.
Tuesday, 11 June 2013
The Three Gables
In this instance our Three Gables refer to men of the mathematical world rather than a house in Harrow Weald; Newton, Hamilton and Lagrange.
Let us take the example of the simple pendulum and the three mathematicians' approaches to finding the equations of motion for this dynamical system. The pendulum weight has mass $m$, $\mathbf{x}$ denotes its position vector, $\dot{\mathbf{x}}$ its velocity vector (i.e. $\frac{d(\mathbf{x})}{dt}=\dot{\mathbf{x}}$) and $\mathbf{p}$ is the momentum vector of the pendulum mass.
Approaches
Newton: Relate a force $\mathbf{F}(\mathbf{x}, \dot{\mathbf{x}}, t)$ to the resulting motion using Newton's 2nd law: $F=ma$ or more appropriately $$\frac{d}{dt}m\dot{\mathbf{x}} = \mathbf{F}(\mathbf{x}, \dot{\mathbf{x}}, t).$$
Lagrange: Construct the Lagrangian function $\mathcal{L}(q, \dot{q},t)$ which can normally be given by $\mathcal{L} = T - V$ where $T$ and $V$ are the kinetic and potential energy of the system respectively. The equations of motion are given by the Euler-Lagrange equation: $$ \frac{d\mathcal{L}}{dq_i} - \frac{d}{dt} \left( \frac{d\mathcal{L}}{d\dot{q}_i} \right) = 0.$$
Hamilton: Construct the Hamiltonian function $H(\mathbf{x}, \mathbf{p},t)$, which is a function of a set of conjugate variable pairs. The Hamiltonian contains the dynamics of the system and Hamilton's equations provide the equations of motion: $$ \frac{d\mathbf{x}_i}{dt} = \frac{\partial H}{\partial \mathbf{x}_i}, $$ $$ \frac{d\mathbf{p}_i}{dt} = \frac{\partial H}{\partial \mathbf{p}_i}. $$
1: Newtonian Mechanics
This is the familiar method for most of us. I have dropped the bold font for vectors from here on.
The force on the pendulum mass is given by $F = -kx$ where $k$ is a constant given by $$k = \omega^2 m $$. Thus we can write $$F=-\omega^2 m.$$
Using Newton's 2nd law we get the equation of motion: $$ m \frac{d}{dt} \dot{x} = -m \omega^2 x, $$ which is equivalent to $$ \frac{d^2 x}{dt^2} = - \omega^2x.$$
The solution to this equation is the standard, two constant oscillatory equation: $$ x(t) = x_0 sin(\omega t + \phi_0)$$ where $x_0$ and $\phi_0$ are constants determined by the inital values of $x(t)$ and $\dot{x}(t)$.
2: Lagrangian Mechanics
The pendulum mass has a kinetic energy: $$T = \frac{1}{2} m \dot{x}^2 $$ and a potential energy given by $$V = \frac{1}{2}m \omega^2 x^2.$$
The Lagrangian in this case may be found using $\mathcal{L} = T-V$: $$\mathcal{L} = T-V = \frac{1}{2} m \dot{x}^2 - \frac{1}{2}m \omega^2 x^2. $$
Using the Euler-Lagrange equation: $$ \frac{d\mathcal{L}}{dx_i} - \frac{d}{dt}\left( \frac{d\mathcal{L}}{d\dot{x}_i}\right) = 0.$$
we can do this step by step:
$$ \frac{d\mathcal{L}}{dx_i} = -\omega^2 mx,$$
and:
$$ \frac{d\mathcal{L}}{d\dot{x}_i}=m\dot{x}.$$
Substituting into the Euler-Lagrange equation we have:
$$-\omega^2 m x - \frac{d}{dt}(m\dot{x}) = 0$$
which is equivalent to:
$$\frac{d^2 x}{dt^2} = -\omega^2 x.$$
Which unsurprisingly is equivalent to our Newtonian formulation and has the same standard oscillatory solution.
3: Hamiltonian
Here we need to use the conjugate pair of position $x_i$ and momentum $p_i$. Given the Lagrangian $\mathcal{L}$, the conjugate momentum and Hamiltonian can be derived as follows:
$$p_i = \frac{\partial \mathcal{L}}{\partial \dot{q}_i} = \frac{\partial \mathcal{L}}{\partial \dot{x}_i} = m\dot{x},$$
$$H = \sum_i \dot{q_i}{p_i} - \mathcal{L} = \sum_i \dot{x}_i p_i - \mathcal{L},$$
which leads to:
$$H = \dot{x}p_x - \mathcal{L} = m\dot{x}^2 - \mathcal{L},$$
and finally we have the Hamiltonian:
$$H = \frac{p^2_x}{2m} + \frac{1}{2}m \omega^2 x^2.$$
Using Hamilton's equations:
$$\frac{dx}{dt} = \frac{\partial H}{\partial p_x} = \frac{p_x}{m}, $$
$$\frac{d p_x}{dt}=-\frac{\partial H}{\partial x} = -m \omega^2 x. $$
Note that the last equation is equivalent to Newton's second law.
Remarks
Using Newtonian mechanics, given the function $\mathbf{F}$, we derive the equations of motion, which must be solved to give the explicit dependence of position $x$ (and thus velocity $\dot{x}$) on the independent parameter $t$.
The physics is constructing the form of $\mathbf{F}$ for a gvien system.
Using Lagrangian mechanics the variables $q_i$ can be any convenient set of parameters that describe the system state. We treat $q_i$ and $\dot{q}_i$ as independent variables, despite the fact that they are not. For $n$ degrees of freedom, the Euler-Lagrange equations give us $n$ second-order differential equations.
The physics is constructing the form of $\mathcal{L}$ for a given system.
Using Hamiltonian mechanics a set of conjugate variables that describe the system state must be carefully chosen. We treat the conjugate pair $x,p_x$ as independent variables despite the fact that they are related. For $n$ degrees of freedom, Hamilton's equations give us $2n$ first-order differential equations. Representing the dynamics using first-order differential equations has some advantages when considering linear methods.
The Hamiltonian is conserved if the independent variable does not appear explicitly in the Hamiltonian. This can be shown:
$$\frac{dH}{dt} = \frac{\partial H}{\partial x}\frac{dx}{dt} + \frac{\partial H}{\partial p_x}\frac{d p_x}{dt} + \frac{\partial H}{\partial t}$$
substituting in Hamilton's equations the first two terms cancel:
$$\frac{dH}{dt} = \frac{\partial H}{\partial x}\frac{\partial H}{\partial p_x} + \frac{\partial H}{\partial p_x}\frac{\partial H}{\partial x} + \frac{\partial H}{\partial t} = \frac{\partial H}{\partial t}.$$
If the Hamiltonian does not depend explicitly on $t$, then the Hamiltonian is conserved:
$$\frac{dH}{dt} = \frac{\partial H}{\partial t} = 0.$$
For our system the Hamiltonian could be written: $$H = T + V, $$
which shows that the Hamiltonian appears to be the total energy of the system.
References
[1] Linear Dynamics, Lecture 1: Review of Hamiltonian Mechanics, Andy Wolski, 2006 [Cockcroft lecture series]
[2] Introduction to Beam Dynamics, Rob Appleby, 2011 [Cockcroft lecture series]
Let us take the example of the simple pendulum and the three mathematicians' approaches to finding the equations of motion for this dynamical system. The pendulum weight has mass $m$, $\mathbf{x}$ denotes its position vector, $\dot{\mathbf{x}}$ its velocity vector (i.e. $\frac{d(\mathbf{x})}{dt}=\dot{\mathbf{x}}$) and $\mathbf{p}$ is the momentum vector of the pendulum mass.
Approaches
Newton: Relate a force $\mathbf{F}(\mathbf{x}, \dot{\mathbf{x}}, t)$ to the resulting motion using Newton's 2nd law: $F=ma$ or more appropriately $$\frac{d}{dt}m\dot{\mathbf{x}} = \mathbf{F}(\mathbf{x}, \dot{\mathbf{x}}, t).$$
Lagrange: Construct the Lagrangian function $\mathcal{L}(q, \dot{q},t)$ which can normally be given by $\mathcal{L} = T - V$ where $T$ and $V$ are the kinetic and potential energy of the system respectively. The equations of motion are given by the Euler-Lagrange equation: $$ \frac{d\mathcal{L}}{dq_i} - \frac{d}{dt} \left( \frac{d\mathcal{L}}{d\dot{q}_i} \right) = 0.$$
Hamilton: Construct the Hamiltonian function $H(\mathbf{x}, \mathbf{p},t)$, which is a function of a set of conjugate variable pairs. The Hamiltonian contains the dynamics of the system and Hamilton's equations provide the equations of motion: $$ \frac{d\mathbf{x}_i}{dt} = \frac{\partial H}{\partial \mathbf{x}_i}, $$ $$ \frac{d\mathbf{p}_i}{dt} = \frac{\partial H}{\partial \mathbf{p}_i}. $$
1: Newtonian Mechanics
This is the familiar method for most of us. I have dropped the bold font for vectors from here on.
The force on the pendulum mass is given by $F = -kx$ where $k$ is a constant given by $$k = \omega^2 m $$. Thus we can write $$F=-\omega^2 m.$$
Using Newton's 2nd law we get the equation of motion: $$ m \frac{d}{dt} \dot{x} = -m \omega^2 x, $$ which is equivalent to $$ \frac{d^2 x}{dt^2} = - \omega^2x.$$
The solution to this equation is the standard, two constant oscillatory equation: $$ x(t) = x_0 sin(\omega t + \phi_0)$$ where $x_0$ and $\phi_0$ are constants determined by the inital values of $x(t)$ and $\dot{x}(t)$.
2: Lagrangian Mechanics
The pendulum mass has a kinetic energy: $$T = \frac{1}{2} m \dot{x}^2 $$ and a potential energy given by $$V = \frac{1}{2}m \omega^2 x^2.$$
The Lagrangian in this case may be found using $\mathcal{L} = T-V$: $$\mathcal{L} = T-V = \frac{1}{2} m \dot{x}^2 - \frac{1}{2}m \omega^2 x^2. $$
Using the Euler-Lagrange equation: $$ \frac{d\mathcal{L}}{dx_i} - \frac{d}{dt}\left( \frac{d\mathcal{L}}{d\dot{x}_i}\right) = 0.$$
we can do this step by step:
$$ \frac{d\mathcal{L}}{dx_i} = -\omega^2 mx,$$
and:
$$ \frac{d\mathcal{L}}{d\dot{x}_i}=m\dot{x}.$$
Substituting into the Euler-Lagrange equation we have:
$$-\omega^2 m x - \frac{d}{dt}(m\dot{x}) = 0$$
which is equivalent to:
$$\frac{d^2 x}{dt^2} = -\omega^2 x.$$
Which unsurprisingly is equivalent to our Newtonian formulation and has the same standard oscillatory solution.
3: Hamiltonian
Here we need to use the conjugate pair of position $x_i$ and momentum $p_i$. Given the Lagrangian $\mathcal{L}$, the conjugate momentum and Hamiltonian can be derived as follows:
$$p_i = \frac{\partial \mathcal{L}}{\partial \dot{q}_i} = \frac{\partial \mathcal{L}}{\partial \dot{x}_i} = m\dot{x},$$
$$H = \sum_i \dot{q_i}{p_i} - \mathcal{L} = \sum_i \dot{x}_i p_i - \mathcal{L},$$
which leads to:
$$H = \dot{x}p_x - \mathcal{L} = m\dot{x}^2 - \mathcal{L},$$
and finally we have the Hamiltonian:
$$H = \frac{p^2_x}{2m} + \frac{1}{2}m \omega^2 x^2.$$
Using Hamilton's equations:
$$\frac{dx}{dt} = \frac{\partial H}{\partial p_x} = \frac{p_x}{m}, $$
$$\frac{d p_x}{dt}=-\frac{\partial H}{\partial x} = -m \omega^2 x. $$
Note that the last equation is equivalent to Newton's second law.
Remarks
Using Newtonian mechanics, given the function $\mathbf{F}$, we derive the equations of motion, which must be solved to give the explicit dependence of position $x$ (and thus velocity $\dot{x}$) on the independent parameter $t$.
The physics is constructing the form of $\mathbf{F}$ for a gvien system.
Using Lagrangian mechanics the variables $q_i$ can be any convenient set of parameters that describe the system state. We treat $q_i$ and $\dot{q}_i$ as independent variables, despite the fact that they are not. For $n$ degrees of freedom, the Euler-Lagrange equations give us $n$ second-order differential equations.
The physics is constructing the form of $\mathcal{L}$ for a given system.
Using Hamiltonian mechanics a set of conjugate variables that describe the system state must be carefully chosen. We treat the conjugate pair $x,p_x$ as independent variables despite the fact that they are related. For $n$ degrees of freedom, Hamilton's equations give us $2n$ first-order differential equations. Representing the dynamics using first-order differential equations has some advantages when considering linear methods.
The Hamiltonian is conserved if the independent variable does not appear explicitly in the Hamiltonian. This can be shown:
$$\frac{dH}{dt} = \frac{\partial H}{\partial x}\frac{dx}{dt} + \frac{\partial H}{\partial p_x}\frac{d p_x}{dt} + \frac{\partial H}{\partial t}$$
substituting in Hamilton's equations the first two terms cancel:
$$\frac{dH}{dt} = \frac{\partial H}{\partial x}\frac{\partial H}{\partial p_x} + \frac{\partial H}{\partial p_x}\frac{\partial H}{\partial x} + \frac{\partial H}{\partial t} = \frac{\partial H}{\partial t}.$$
If the Hamiltonian does not depend explicitly on $t$, then the Hamiltonian is conserved:
$$\frac{dH}{dt} = \frac{\partial H}{\partial t} = 0.$$
For our system the Hamiltonian could be written: $$H = T + V, $$
which shows that the Hamiltonian appears to be the total energy of the system.
References
[1] Linear Dynamics, Lecture 1: Review of Hamiltonian Mechanics, Andy Wolski, 2006 [Cockcroft lecture series]
[2] Introduction to Beam Dynamics, Rob Appleby, 2011 [Cockcroft lecture series]
Monday, 10 June 2013
LaTeX in Blogger
Sunday, 5 May 2013
United Nations office in Geneva
The Assembly Hall - the largest room in the Palace of Nations.
The Human Rights and Alliance of Civilisations Room, decorated by famous artist Miquel Barcelo - see how the ceiling was made by clicking here.
The Council Chamber, where many important historical negotiations have taken place, with murals by Jose Maria Sert.
Peak District: Edale (March 2012)
Members of the NGACDT visited Huddersfield in March 2012. Anna Kolano had the idea of going for a hike in the peak district.

Panos is visible taking a photograph to the right of the middle. The rest of the group are sat on a large rock to the right of the image.

The group is visible on the left of the image.
Anna is visible to the right of the image, and Rob, Amanda and Manu are visible on the left.
The small dots in the sky to the left are paragliders.
CERN 2012
A few images taken at The European Centre for Nuclear Research (CERN) in the summer of 2012.
The view from the LHCb flat in Meyrin. The Jura mountains are visible on the right.
The magnet testing facility at point 2.
The main CERN site in Meyrin. The CERN Globe is visible over the farms.
The CERN Prevessin site entrance. The Jura mountains are visible in the background.
Prevessin site entrance.
Magnet testing facility.
Magnet testing facility.
Magnet testing facility. The large blue apparatus in an LHC dipole.
Geneva 2012
A few panoramic images taken around Lake Geneva.
Inside the Ariana Museum.
Lake Geneva - note the parrot sat on the white-shirted man's shoulder.
Lake Geneva.
Lake Geneva with the Jet D'eau.
Lake Geneva with the Jet D'eau and Mont Blanc.
Lake Geneva with the Jet D'eau and Mont Blanc.
Lake Geneva.
Outside the science museum in Parc du Lac.
Outside the science museum in Parc du Lac.
Glasgow
The NGACDT annual conference took place at the University of Strathclyde in Glasgow in September 2012. Here are a few panoramic images stitched from images taken at Glasgow University.
Monday, 11 March 2013
Match Report: HUD Mens 1st vs Bradford 1st
Here follows a critical review of the University of Huddersfield Mens 1st team performance on 06.03.13.
The final game of the season started with a full house. Two (debatable) referees were present at the game.
The first quarter saw Huddersfield start with strong defensive energy. A starting five of Misters: Legros, Babalola, Moore, Piskorz, and Surkus. Despite slow progress in terms of points, Bradford No. 13 was benched due to his 3 fouls - Bradford in fact committing 6 fouls in the quarter. For the home team Mr. Surkus lead the scoring with an aggressive 7 out of 13 points. The quarter ended 13-12 with Bradford the clear underdogs.
At the start of the second quarter Bradford decided to bring in an outside offence, with No. 7 totalling 12 points in the quarter. Coupled with some sloppy offence and a few turnovers from the home team, Huddersfield's energy had been zapped by Bradford's prowess at the three point line. The quarter ended 27-28 to Bradford.
Following a hearty speech from coach Mark Mills at half time; "They have more energy than us! F**K THAT! ...", Huddersfield picked up the pace in the second half. Despite more energy Bradford managed to hold on to the lead - more due to poor defence than strong offence. A close end to the third quarter 37-39 to Bradford.
The final quarter belonged to the fans. A downhearted Huddersfield team began the final quarter with even more energy; spurred on by the chants of "DEFENCE, DEFENCE..." at every Bradford possession, Huddersfield forced many turn overs. The one sided refereeing tipped to Huddersfield's favour as three Bradford players were fouled out, however this did not last long. Despite the horrendous crimes to humanity committed by the disillusioned and most likely intoxicated referees, the home team kept their heads up. The home team found themselves 6 points down with 56 seconds left on the clock.
Thanks to strong defence and quick hands from Mr. Piskorz, and an outstanding effort from the home team, the scores were even with only a few seconds left. Coach Mark Mills had used a full court press to great effect for the majority of the final quarter - it paid dividends as Huddersfield gained possession and were fouled at every opportunity - Bradford ended the final quarter with over 10 team fouls and a total greater than 25 team fouls. Despite some sloppy free throw shooting, an ecstatic Huddersfield took and held the lead to finish 60-56. The crowd roared as the supporting members of them team flew from the stands and congratulated their team mates; in less than a minute they had gone on a 10 point streak.
An entertaining and thrilling end to the season sees Huddersfield Mens 1st team promoted to the BUCS Northern 2B league. Another season like this and Coach Mark Mills may need hair implants. In the words of an anonymous team member; what followed was a 'messy night'.

| No | Points | Fouls | |
| James Deakin | 4 | 0 | 0 |
| Ivan Robles | 5 | 0 | 1 |
| Eimantis Lukauskis | 6 | 0 | 3 |
| Kehinde Babalola | 7 | 4 | 2 |
| Kamil Piskorz | 8 | 16 | 3 |
| Yannick Legros | 9 | 10 | 0 |
| Hassan Haq | 10 | 0 | 0 |
| Robert Senior | 11 | 6 | 1 |
| NaurisAgafonovs | 12 | 6 | 1 |
| Airidas Surkus | 13 | 8 | 1 |
| Dan Moore Amr Ibrahim | 14 15 | 10 0 | 1 0 |
| Total | 60 | 13 |
| Q1 | Q2 | Q3 | Q4 | |
| HUD | 13 | 27 | 37 | 60 |
| BRD | 12 | 28 | 39 | 56 |
The final game of the season started with a full house. Two (debatable) referees were present at the game.
The first quarter saw Huddersfield start with strong defensive energy. A starting five of Misters: Legros, Babalola, Moore, Piskorz, and Surkus. Despite slow progress in terms of points, Bradford No. 13 was benched due to his 3 fouls - Bradford in fact committing 6 fouls in the quarter. For the home team Mr. Surkus lead the scoring with an aggressive 7 out of 13 points. The quarter ended 13-12 with Bradford the clear underdogs.
At the start of the second quarter Bradford decided to bring in an outside offence, with No. 7 totalling 12 points in the quarter. Coupled with some sloppy offence and a few turnovers from the home team, Huddersfield's energy had been zapped by Bradford's prowess at the three point line. The quarter ended 27-28 to Bradford.
Following a hearty speech from coach Mark Mills at half time; "They have more energy than us! F**K THAT! ...", Huddersfield picked up the pace in the second half. Despite more energy Bradford managed to hold on to the lead - more due to poor defence than strong offence. A close end to the third quarter 37-39 to Bradford.
The final quarter belonged to the fans. A downhearted Huddersfield team began the final quarter with even more energy; spurred on by the chants of "DEFENCE, DEFENCE..." at every Bradford possession, Huddersfield forced many turn overs. The one sided refereeing tipped to Huddersfield's favour as three Bradford players were fouled out, however this did not last long. Despite the horrendous crimes to humanity committed by the disillusioned and most likely intoxicated referees, the home team kept their heads up. The home team found themselves 6 points down with 56 seconds left on the clock.
Thanks to strong defence and quick hands from Mr. Piskorz, and an outstanding effort from the home team, the scores were even with only a few seconds left. Coach Mark Mills had used a full court press to great effect for the majority of the final quarter - it paid dividends as Huddersfield gained possession and were fouled at every opportunity - Bradford ended the final quarter with over 10 team fouls and a total greater than 25 team fouls. Despite some sloppy free throw shooting, an ecstatic Huddersfield took and held the lead to finish 60-56. The crowd roared as the supporting members of them team flew from the stands and congratulated their team mates; in less than a minute they had gone on a 10 point streak.
An entertaining and thrilling end to the season sees Huddersfield Mens 1st team promoted to the BUCS Northern 2B league. Another season like this and Coach Mark Mills may need hair implants. In the words of an anonymous team member; what followed was a 'messy night'.

Tuesday, 12 February 2013
Panorama: Home
Panoramic images convey entire landscapes in a single image. Here are a few that I have constructed using Hugin Panorama Creator (linux).
The Naden and Greenbooth reservoirs are where I go running on a fine summers day. In 2008 a wind farm was constructed.
Subscribe to:
Comments (Atom)





































.png)
.png)
.png)
.png)
.png)




