1. Coordinates

We begin by defining a curved coordinate system, the curvature $\rho$ produced by a local dipole field, and the path length along the design trajectory is $s$. The position of a particle in these coordinates is:

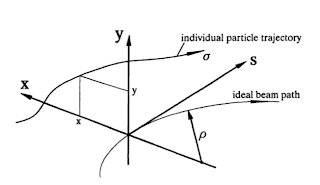
Circular coordinate system [1]

\begin{equation} \vec{R} ~=~ r \vec{x} + y \vec{z}, \end{equation}

where
\begin{equation} r ~=~ \rho + x. \end{equation}
These coordinates represent deviations with respect to the ideal design orbit, we assume these deviations to be small; in reality $x$ is in the of order mm. We use the positions $x$ and $y$, and their slopes $x' = \frac{dx}{ds}$ and $y' = \frac{dy}{ds}$.

Circular coordinate system [2]

References

[1] R. Appleby. Beam Dynamics. Cockcroft Lectures 2011

[2] H. Weidemann. Particle Accelerator Physics I: Basic Principles and Linear Beam

Dynamics. Springer, 1999